---

ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ

1) Если log_ab = c, то а^c = b. Это можно представить в виде следующей схемы (источник: Видеоуроки, презентации для учителя):

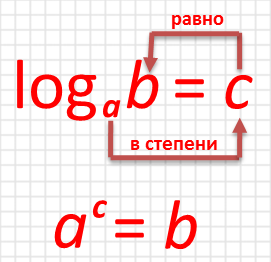
2) При решении логарифмических уравнений обязательно делать проверку или проверять корни на принадлежность к области определения!

3) Как решать квадратные уравнения.

---

РЕШЕНИЕ

. По вышеприведенной схеме имеем:

(х - 5)² = 49, откуда
х - 5 = 7 или х - 5 = -7

Решая эти два уравнения, имеем х₁ = 12 и х₂ = -2.

Проверка.
х₁ = 12:  log_12-549 = 2;  log₇49 = 2;   2=2.
х₂ = -2: log_-2-549 = 2; log_-749 = 2; корень не подходит, поскольку основание логарифма не может быть отрицательным.

Итак, уравнение имеет единственный корень 12.

Ответ: 12.

P.S. Это задание с подвохом для тех, кто не сделает проверку. Они напишут в ответ -2 и потеряют свои баллы.

---