Mat-EGE.ru - решение прототипов ЕГЭ-2012 по математике
Выберите категорию прототипов для просмотра решения
B2 B6 B7 B8 B9 B11 B13 B14
B1 B3 B4 B5 B10 B12




Бесплатные видеоуроки по ЕГЭ математика-2012
Ваш e-mail: *
Ваше имя: *
ЕГЭ по математике » Решения ЕГЭ-прототипов и задач по математике » Прототипы части B » Решения прототипов B6
Решение прототипа №27260 (B6)
Просмотров: 6911

В треугольнике ABC угол C равен 90^\circ, CH  — высота, AB = 27, \sin A = \frac{2}{3}. Найдите BH.

Иллюстрация к решению прототипа №27421

ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ

1) Обратите внимание на рисунок треугольника АВС выше. Угол В равен углу НСА, угол А равен углу ВСН.
Треугольники АВС, АСН и СВН подобны - это значит, что у них пропорционально относятся соответствующие стороны. (Задача решается без использования подобия, но этот способ тоже годится).

2) Катет, прилежащий углу, равен произведению гипотенузы на косинус угла.

3) Основное тригонометрическое тождество sin2A + cos2A = 1.

РЕШЕНИЕ

Рисунок к задаче см. на карточке-подсказке выше.

1) Сначала найдем АН.

Из прямоугольного треугольника ACH: Катет (АН), прилежащий углу (А), равен произведению гипотенузы (АС) на косинус угла (А):

АН = АС·cos A (*)

Из прямоугольного треугольника ABC: Катет (АC), прилежащий углу (А), равен произведению гипотенузы (АB) на косинус угла (А):

АC = АB·cos A (**)

Подставим выражение (**) в (*):

АН = АС·cos A = (АB·cos A)·cos A = АВ·cos2 A.

Из основного тригонометрического тождества найдем cos2 A, затем, умножив на АВ, найдем АН:

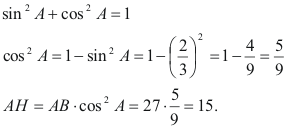
Иллюстрация к решению прототипа №27259

2) ВН = АВ - АН = 27 - 15 = 12.

Ответ: 12
Понравилось? Нажми:
Твитнуть
Нравится


Комментарии с нецензурной лексикой, оскорбления, а также
вопросы типа "а где решение?" останутся без ответа и/или будут удаляться.
Чтобы найти решение, внимательно читайте крупные красные буквы выше.
Для особо одаренных: решение здесь или здесь.
(Если вдруг не открывается, попробуйте чуть позже).

Копирование решений прототипов на другие сайты запрещено
   Данное решение экзаменационного задания по математике составлено администрацией сайта Mat-EGE.Ru. Мы искренне желаем всем будущим выпускникам, которые смотрят данную страницу, повысить свой уровень по математике и сдать Единый государственный экзамен на достойную оценку, поступить в желаемый вуз, зарабатывать деньги на высокооплачиваемой работе и быть достойным гражданином своего государства. Добиваемся успеха вместе!


Ответы ЕГЭ по математике 2013











© https://mat-ege.ru, 2018. Использованы материалы сайта Открытого банка заданий по математике. Хостинг от uCoz
Копирование решений задач на другие сайты категорически запрещено законодательством РФ об авторском праве.
В случае нарушения наших прав администрация не поленится собщить в правоохранительные органы.