---

ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ

1) Углы, сумма которых 90^о, (в нашей задаче В и ВАН) называются дополнительными. Дополнительные углы обладают такими свойствами:
sin B = cos BAH,       cos B = sin BAH,               tg B = ctg BAH,                ctg B = tg BAH

2) В равнобедренном треугольнике углы при основании равны (в нашей задаче это углы В и ВАС).

3) Основные тригонометрические формулы

;

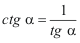4) У острых углов и синусы, и косинусы положительные.

---

РЕШЕНИЕ

Рисунок к задаче см. на карточке-подсказке выше.

tg BAH = ctg B = сtg BAС, т.к. углы ВАН и В дополнительные (см. п.1 "Что необходимо знать для решения"), а углы ВАС и В равны (см. п.2 "Что необходимо знать для решения").

Итак: tg BAH = сtg BAС. Найдем ctg BAС по тригонометрическим формулам из п.3 "Что необходимо знать для решения":

tg BAH = ctg BAC = 0,25

Ответ: 0,25

---