Катеты равнобедренного прямоугольного треугольника равны 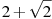 . Найдите радиус окружности, вписанной в этот треугольник.
. Найдите радиус окружности, вписанной в этот треугольник.
ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ
1) Диагональ квадрата равна стороне, умноженной на .
.
2) Медиана, проведенная к гипотенузе, равна половине гипотенузы.
3) В равнобедренном треугольнике медиана является биссектрисой и высотой.
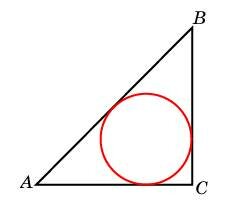
РЕШЕНИЕ

По условию, АС = ВС = 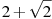 . Проведем CM - медиану, биссектрису и высоту треугольника АВС. Поскольку СМ - биссектриса, она пройдет через О - центр вписанной окружности, а поскольку СМ - высота, она совпадет с радиусом ОМ. (Найти нужно радиус OM = ON = OK).
. Проведем CM - медиану, биссектрису и высоту треугольника АВС. Поскольку СМ - биссектриса, она пройдет через О - центр вписанной окружности, а поскольку СМ - высота, она совпадет с радиусом ОМ. (Найти нужно радиус OM = ON = OK).
1) Найдем гипотенузу треугольника АВС:

2) Т.к. медиана прямоугольного треугольника МС, проведенная к гипотенузе АВ, равна половине гипотенузы, то

3) Пусть радиус вписанной окружности равен х, тогда OM = x. Четырехугольник OKCN - квадрат, его диагональ OC равна стороне ON, умноженной на . Поэтому:
. Поэтому:

Итак, радиус вписанной окружности в треугольник равен 1.
Ответ: 1



