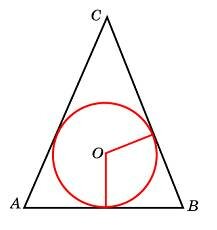
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ
1) В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
2) Признак равенства прямоугольных треугольников:
Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.
РЕШЕНИЕ

По условию, CN = 5, NB = 3. Проведем CK - медиану, биссектрису и высоту равнобедренного треугольника АВС. Поскольку CK - биссектриса, она пройдет через О - центр вписанной окружности. Поскольку CK - высота, она совпадет с перпендикуляром OK.
1) Прямоугольные треугольники OKB и ONB равны по гипотенузе и катету. Действительно, OB - общая для них гипотенуза, ONB и OKB - прямые углы, а катеты ON и OK равны как радиусы одной окружности. Следовательно, NB = KB = 3.
2) Поскольку CK - медиана, то AB = 2KB = 2 · 3 = 6.
3) ВС = 5 + 3 = 8, по условию АС = ВС = 8. Следовательно, искомый периметр равен АС + ВС + АВ = 8 + 8 + 6 = 22.
Ответ: 22



