Mat-EGE.ru - решение прототипов ЕГЭ-2012 по математике
Выберите категорию прототипов для просмотра решения
B2 B6 B7 B8 B9 B11 B13 B14
B1 B3 B4 B5 B10 B12




Бесплатные видеоуроки по ЕГЭ математика-2012
Ваш e-mail: *
Ваше имя: *
ЕГЭ по математике » Решения ЕГЭ-прототипов и задач по математике » Прототипы части B » Решения прототипов B6
Решение прототипа №27937 (B6)
Просмотров: 17148

Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

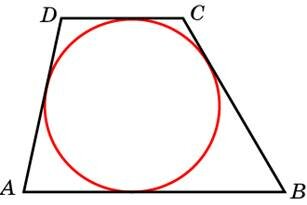
MA.OB10.B4.320/innerimg0.jpg

ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ

1) Суммы противолежащих сторон выпуклого четырехугольника, описанного около окружности, равны.
2) Средняя линия трапеции равна полусумме оснований.

РЕШЕНИЕ

Т.к. суммы противолежащих сторон выпуклого четырехугольника, описанного около окружности, равны, то AD + BC = AB + CD = 40 : 2  = 20. Итак, сумма оснований AB + CD равна 20. Поскольку средняя линия трапеции равна полусумме оснований, то она равна 20 : 2 = 10

Ответ: 10
Понравилось? Нажми:
Твитнуть
Нравится


Комментарии с нецензурной лексикой, оскорбления, а также
вопросы типа "а где решение?" останутся без ответа и/или будут удаляться.
Чтобы найти решение, внимательно читайте крупные красные буквы выше.
Для особо одаренных: решение здесь или здесь.
(Если вдруг не открывается, попробуйте чуть позже).

Копирование решений прототипов на другие сайты запрещено
   Данное решение экзаменационного задания по математике составлено администрацией сайта Mat-EGE.Ru. Мы искренне желаем всем будущим выпускникам, которые смотрят данную страницу, повысить свой уровень по математике и сдать Единый государственный экзамен на достойную оценку, поступить в желаемый вуз, зарабатывать деньги на высокооплачиваемой работе и быть достойным гражданином своего государства. Добиваемся успеха вместе!


Ответы ЕГЭ по математике 2013











© https://mat-ege.ru, 2018. Использованы материалы сайта Открытого банка заданий по математике. Хостинг от uCoz
Копирование решений задач на другие сайты категорически запрещено законодательством РФ об авторском праве.
В случае нарушения наших прав администрация не поленится собщить в правоохранительные органы.