Mat-EGE.ru - решение прототипов ЕГЭ-2012 по математике
Выберите категорию прототипов для просмотра решения
B2 B6 B7 B8 B9 B11 B13 B14
B1 B3 B4 B5 B10 B12




Бесплатные видеоуроки по ЕГЭ математика-2012
Ваш e-mail: *
Ваше имя: *
ЕГЭ по математике » Решения ЕГЭ-прототипов и задач по математике » Прототипы части B » Решения прототипов B6
Решение прототипа №27938 (B6)
Просмотров: 26557

Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.

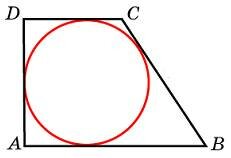
MA.OB10.B4.321/innerimg0.jpg

ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ

1) Суммы противолежащих сторон выпуклого четырехугольника, описанного около окружности, равны.
2) Средняя линия трапеции равна полусумме оснований.

РЕШЕНИЕ

Иллюстрация к решению прототипа №27938

Т.к. суммы противолежащих сторон выпуклого четырехугольника, описанного около окружности, равны, то AD + BC = AB + CD = 22 : 2 = 11. Итак, сумма боковых сторон AD + BC равна 11, откуда AD = 11 - BC = 11 - 7 = 4.

Поскольку сторона AD = 4 равна диаметру вписанной окружности, то радиус ее равен AD : 2 =4 : 2 = 2.

Ответ: 2
Понравилось? Нажми:
Твитнуть
Нравится


Комментарии с нецензурной лексикой, оскорбления, а также
вопросы типа "а где решение?" останутся без ответа и/или будут удаляться.
Чтобы найти решение, внимательно читайте крупные красные буквы выше.
Для особо одаренных: решение здесь или здесь.
(Если вдруг не открывается, попробуйте чуть позже).

Копирование решений прототипов на другие сайты запрещено
   Данное решение экзаменационного задания по математике составлено администрацией сайта Mat-EGE.Ru. Мы искренне желаем всем будущим выпускникам, которые смотрят данную страницу, повысить свой уровень по математике и сдать Единый государственный экзамен на достойную оценку, поступить в желаемый вуз, зарабатывать деньги на высокооплачиваемой работе и быть достойным гражданином своего государства. Добиваемся успеха вместе!


Ответы ЕГЭ по математике 2013











© https://mat-ege.ru, 2019. Использованы материалы сайта Открытого банка заданий по математике. Хостинг от uCoz
Копирование решений задач на другие сайты категорически запрещено законодательством РФ об авторском праве.
В случае нарушения наших прав администрация не поленится собщить в правоохранительные органы.