Mat-EGE.ru - решение прототипов ЕГЭ-2012 по математике
Выберите категорию прототипов для просмотра решения
B2 B6 B7 B8 B9 B11 B13 B14
B1 B3 B4 B5 B10 B12




Бесплатные видеоуроки по ЕГЭ математика-2012
Ваш e-mail: *
Ваше имя: *
ЕГЭ по математике » Решения ЕГЭ-прототипов и задач по математике » Прототипы части B » Решения прототипов B6
Решение прототипа №27940 (B6)
Просмотров: 21661

Периметр четырехугольника, описанного около окружности, равен 24, две его стороны равны 5 и 6. Найдите большую из оставшихся сторон.

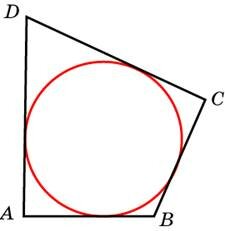
MA.OB10.B4.323/innerimg0.jpg

ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ

Суммы противолежащих сторон выпуклого четырехугольника, описанного около окружности, равны.

РЕШЕНИЕ

Т.к. AB + CD = AD + BC (см. "Что необходимо знать для решения") то если периметр равен 24, то сумма противолежащих сторон равна 24 : 2 = 12. Нам даны две стороны 5 и 6, их сумма равна 11, а не 12, значит, эти стороны не противоположные.

Сторона, противоположная стороне 5, равна 12 - 5 = 7.
Сторона, противоположная стороне 6, равна 12 - 6 = 6.

Таким образом, видим, что большая из оставшихся сторон (противоположная стороне 5), равна 7.

Ответ: 7
Понравилось? Нажми:
Твитнуть
Нравится


Комментарии с нецензурной лексикой, оскорбления, а также
вопросы типа "а где решение?" останутся без ответа и/или будут удаляться.
Чтобы найти решение, внимательно читайте крупные красные буквы выше.
Для особо одаренных: решение здесь или здесь.
(Если вдруг не открывается, попробуйте чуть позже).

Копирование решений прототипов на другие сайты запрещено
   Данное решение экзаменационного задания по математике составлено администрацией сайта Mat-EGE.Ru. Мы искренне желаем всем будущим выпускникам, которые смотрят данную страницу, повысить свой уровень по математике и сдать Единый государственный экзамен на достойную оценку, поступить в желаемый вуз, зарабатывать деньги на высокооплачиваемой работе и быть достойным гражданином своего государства. Добиваемся успеха вместе!


Ответы ЕГЭ по математике 2013











© https://mat-ege.ru, 2019. Использованы материалы сайта Открытого банка заданий по математике. Хостинг от uCoz
Копирование решений задач на другие сайты категорически запрещено законодательством РФ об авторском праве.
В случае нарушения наших прав администрация не поленится собщить в правоохранительные органы.