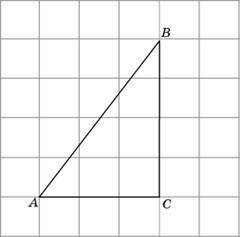
Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.
ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ
1) Формулу  , где r - радиус вписанной окружности; a, b - катеты треугольника; с - его гипотенуза.
, где r - радиус вписанной окружности; a, b - катеты треугольника; с - его гипотенуза.
2) Теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
РЕШЕНИЕ
1) Найдем по теореме Пифагора гипотенузу АВ:

2) По формуле  найдем радиус вписанной окружности:
найдем радиус вписанной окружности:

Ответ: 1
P.S. Треугольник со сторонами 3, 4, 5 называют "египетским треугольником". По теореме Пифагора легко проверить, что этот треугольник прямоугольный: 3
2 + 4
2 = 5
2. Вообще, любой треугольник со сторонами, относящимися как 3 : 4 : 5, будет прямоугольным. Например, треугольник со сторонами 6, 8, 10, или треугольник со сторонами 9, 12, 15.
Этим можно пользоваться при решении задач. Если замечаем, что катеты относятся как 3 : 4, то есть, один содержит 3 "части", а другой 4 "части", то гипотенуза будет содержать 5 таких "частей", и ее легко найти. Теоремой Пифагора в том случае можно не пользоваться. Например, если известно, что один катет равен 6, а другой 8. Замечаем, что 6 : 8 = 3 : 4. Катет 6 содержит 3 "части", а катет 8 содержит 4 "части". Следовательно, одна "часть" равна 2. Гипотенуза содержит 5 "частей" и будет равна 2 · 5 = 10.



