Задач категории B12 решено: 58 из 62
Показано задач: 16-30 |
Страницы: « 1 2 3 4 » |
Сортировать по: Дате · Названию · Рейтингу · Комментариям · Просмотрам
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: 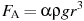 , где , где 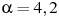 — постоянная, r — радиус аппарата в метрах, — постоянная, r — радиус аппарата в метрах, 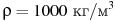 — плотность воды, а g — ускорение свободного падения (считайте — плотность воды, а g — ускорение свободного падения (считайте 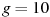 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах. Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.
|
Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: 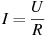 , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах. , где U — напряжение в вольтах, R — сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.
|
|
|



