---

ЧТО НЕОБХОДИМО ЗНАТЬ ДЛЯ РЕШЕНИЯ

1) Некоторые формулы приведения:
sin (180^o - x) = sin x          cos (180^o - x) = - cos x          tg (180^o - x) = -tg x          ctg (180^o - x) = - ctg x
2) Тригонометрическую формулу

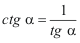
3) Углы, сумма которых 90^о, называются дополнительными. В нашей задаче это углы А и В. Дополнительные углы обладают таким свойством: sin B = cos A. См. также первый столбец формул карточки-подсказки вверху.

---

РЕШЕНИЕ

Рисунок к задаче см. на карточке-подсказке выше.

1) Найдем ctg A по известному тангенсу:

ctg A = 1 : tg A = 1 : 2 = 0,5

2) Поскольку углы А и В треугольника АВС дополнительные, то tg B = ctg A = 0,5.

3) Внешний угол при вершине B - это угол ABM. Поскольку углы ABM и ABC смежные (угол ABC - это и есть угол B) , то ABM = 180^o - ABC, и

tg ABM = tg (180^o - ABC) = -tg ABC (т.е. -tg B) = -0,5

Ответ: -0,5

---