Mat-EGE.ru

Подготовка к ЕГЭ и ОГЭ по математике - 2020

Задания №12 ЕГЭ по математике (нумерация 2012 г)

<< На главную

Решение прототипа 27953

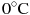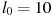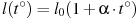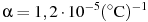При температуре 0^\circ {\rm{C}} рельс имеет длину l_0 =10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(t^\circ ) = l_0 (1 + \alpha \cdot t^\circ ), где \alpha= 1,2\cdot 10^{ - 5}(^\circ {\rm{C}})^{-1}  — коэффициент теплового расширения, t^\circ  — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.

Решение прототипа 27954

Некоторая компания продает свою продукцию по цене 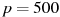p=500 руб. за единицу, переменные затраты на производство одной единицы продукции составляют 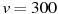v=300 руб., постоянные расходы предприятия 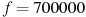f= 700000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле 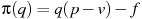\pi(q)=q(p-v)-f. Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300000 руб.

Решение прототипа 27955

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле 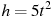h=5t^2, где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.

Решение прототипа 27956

Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p  (тыс. руб.) задаeтся формулой 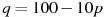q=100-10p. Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле 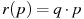r(p)=q\cdot p. Определите наибольшую цену p, при которой месячная выручка 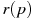r(p) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.

Решение прототипа 27957

Высота над землeй подброшенного вверх мяча меняется по закону 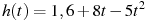h(t)=1,6 + 8t - 5t^2 , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?

Решение прототипа 27958

Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна 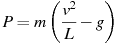P= m\left( {\frac{{v^2 }}{L} - g} \right), где m — масса воды в килограммах, v — скорость движения ведeрка в м/с, L — длина верeвки в метрах, g — ускорение свободного падения (считайте 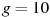g=10м/с{}^2). 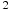С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.

Решение прототипа 27959

В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону 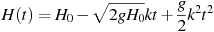H(t) = H_0-\sqrt {2gH_0 } kt + \frac{g}{2}k^2 t^2, где t — время в секундах, прошедшее с момента открытия крана, 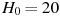H_0=20 м — начальная высота столба воды, 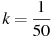k = \frac{1}{{50}} — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте 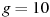g=10 м/с{}^2). 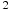Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?

Решение прототипа 27960

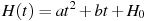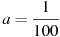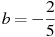В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону H(t) = at^2 + bt + H_0, где H_0 = 4 м — начальный уровень воды, a = \frac{1}{{100}}\  м/мин2, и b=-\frac{2}{5} м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.

Решение прототипа 27961

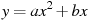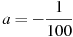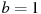Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой y = ax^2 + bx, где a = - \frac{1}{{100}}  м{}^{ - 1}, b=1 — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?

Решение прототипа 27962

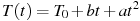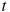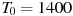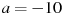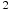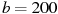Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температур вычисляется по формуле T(t) = T_0 + bt + at^2 , где t — время в минутах, T_0 = 1400 К, a = - 10 К/мин{}^2, b = 200 К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Решение прототипа 27963

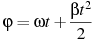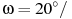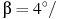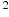Для сматывания кабеля на заводе используют лебeдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону \varphi = \omega t + \frac{{\beta t^2 }}{2}, где t — время в минутах, \omega = 20^\circ/мин — начальная угловая скорость вращения катушки, а \beta = 4^\circ/мин{}^2 — угловое ускорение, с которым наматывается кабель. 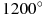Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки \varphi достигнет 1200^\circ. Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.

Решение прототипа 27964

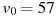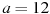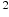Мотоциклист, движущийся по городу со скоростью v_0 = 57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a = 12 км/ч{}^2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением 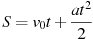S = v_0 t + \frac{{at^2 }}{2}. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.

Решение прототипа 27965

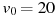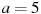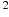Автомобиль, движущийся в начальный момент времени со скоростью v_0 = 20 м/с, начал торможение с постоянным ускорением a = 5 м/с{}^2. За t секунд после начала торможения он прошёл путь 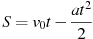S = v_0 t - \frac{{at^2 }}{2} (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.

Решение прототипа 27966

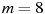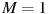Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой m = 8 кг и радиуса R = 10 см, и двух боковых с массами M = 1 кг и с радиусами 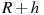R+h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг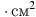\cdot\text{см}^2, даeтся формулой 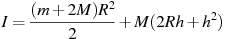I = \frac{{(m + 2M)R^2 }}{2} + M(2Rh + h^2 ). При каком максимальном значении h момент инерции катушки не превышает предельного значения 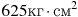625\text{кг}\cdot\text{см}^2? Ответ выразите в сантиметрах.

Решение прототипа 27967

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: 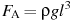F_{\rm{A}} = \rho gl^3, где l — длина ребра куба в метрах, 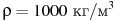\rho = 1000~\text{кг}/\text{м}^3 — плотность воды, а g — ускорение свободного падения (считайте 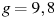g = 9,8 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 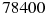78 400 Н? Ответ выразите в метрах.

mat-ege.ru © 2019