Здесь представлены видеоразборы заданий, аналогичных тем, которые предлагались обучающимся 9-х классов для выполнения 5.03.2020 г. Подчёркиваем, что здесь разобраны именно аналоги, а не те же самые задания (во избежание нарушения авторских прав).
Задания 1-5
Условия и решения заданий 1 – 5 Вы можете посмотреть на отдельной странице.
Задания 6 – 15 (алгебра)
| 6. Найдите значение выражения (\frac{17}{35}+\frac{3}{8}):\frac{5}{28} | Смотреть видеоразбор |
7. На координатной прямой отмечены числа a и b.
1) а + b < 0 2) −4 < a − 1 < −3 3) a2b<0 4) -b < 0 |
Смотреть видеоразбор |
| 8. Найдите значение выражения \sqrt{5\cdot18}\cdot\sqrt{30} 1) 30\sqrt{15} 2) 30\sqrt{3} 3) 90 4) 30\sqrt{6} |
Смотреть видеоразбор |
| 9. Решите уравнение 2x^2+12x=0 | Смотреть видеоразбор |
| 10. В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. | Смотреть видеоразбор |
11. Задание изображено на рисунке
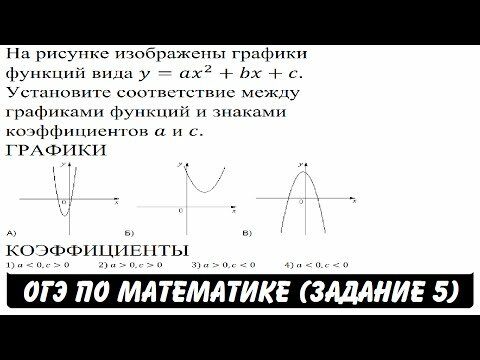
|
Смотреть видеоразбор |
| 12. Выписаны первые несколько членов арифметической прогрессии: 2,6;3,3;4;… Найдите сумму первых 21 её членов. | Смотреть видеоразбор |
| 12а. Выписаны первые несколько членов геометрической прогрессии: 3,5;7; 14;… Найдите сумму первых 7 её членов. | Смотреть видеоразбор |
| 13. Найдите значение выражения \frac{16}{4a-a^2}-\frac{4}{a} при a=-12 | Смотреть видеоразбора |
| 14. В фирме «Эх, прокачу!» стоимость поездки на такси длительностью меньше 5 минут составляет 150 рублей. Если поездка длится 5 минут или более, то её стоимость (в рублях) рассчитывается по формуле C=150+11(t-5), где t – длительность поездки, выраженная в минутах (t≥5). Пользуясь этой формулой, рассчитайте стоимость 10-минутной поездки. Ответ укажите в рублях. | Смотреть видеоразбор |
| 15. Укажите решение неравенства 9x-4(x-7)\ge-3 1) [-6,2; +\infty) \;\;\;\;\;\;\;\; 2) [5; +\infty) \;\;\;\;\;\;\;\; 3) (-\infty; 5] \;\;\;\;\;\;\;\; 4) (-\infty; -6,2] |
Смотреть видеоразбор |
Задания 16-20 (геометрия)
| 16. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 60, сторона BC равна 54, сторона AC равна 72. Найдите MN. | Смотреть видеоразбор |
| 17. Четырёхугольник ABCD описан около окружности,AB = 14, BC = 8, CD = 15. Найдите AD. | Смотреть видеоразбор |
| 18. Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 6, BD = 10, AB = 3,5. Найдите DO. | Смотреть видеоразбор |
| 19. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь. | Смотреть видеоразбор |
|
20. Укажите номера верных утверждений Сумма острых углов прямоугольного треугольника равна 90°. Видеоразбор
|
Часть 2
| 21. Решите неравенство \frac{-19}{(x+5)^2-6}\ge0 | Смотреть видеоразбор |
| 22. Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде? | Смотреть видеоразбор |
| 23. Постройте график функции y=-2+\frac{x+5}{x^2+5x}. Определите, при каких значениях m прямая y=m не имеет с графиком общих точек. |
Смотреть видеоразбор |
| 24. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K . Найдите периметр параллелограмма, если BK = 8, CK = 20. | Смотреть видеоразбор |
| 25. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке О. Докажите, что площади треугольников AОB и CОD равны. | Смотреть видеоразбор |
| 26. Окружности радиусов 25 и 100 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D – на второй. При этом АС и ВD – общие касательные окружностей. Найдите расстояние между прямыми АВ и СD. | Смотреть видеоразбор |
