Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;7), (7;10).

РЕШЕНИЕ
Дополним до прямоугольника, как показано на рисунке (в данном случае получится квадрат):

Площадь искомой фигуры равна разности площадей красного квадрата и трех белых прямоугольных треугольников внутри квадрата.
Площадь квадрата равна 10 · 10 = 100.
Площадь прямоугольного треугольника равна половине произведения его катетов. Следовательно, площади белых треугольников равны 7 · 10 / 2 = 35, 7 · 10 / 2 = 35, 3 · 3 / 2 = 4,5.
Площадь искомого треугольника равна 100 – 35 – 35 – 4,5 = 25,5.
Ответ: 25,5.
 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.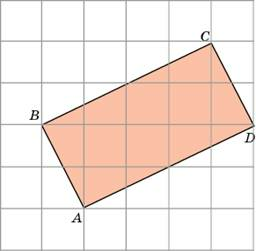

 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.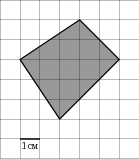

 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.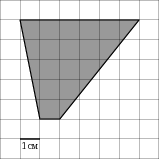
 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.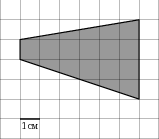
 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

 фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
фигуры, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). В ответе запишите
1 см (см. рис.). В ответе запишите  .
.





